Linguistic Comparisons

Much of what is done is the way of linguistic comparison seems to be a bit subjective. The most favorite is to gather a bunch of idioms and then set them against each other drawing obvious conclusions, like language X is better than Y if you need a way of describing behavior Z. Though interesting in it’s own right (through this technique we can amass a large collection of idioms and probably use them as the building blocks for Domain Specific Languages), it doesn’t achieve as much as I’d like, mostly because of it’s isolated comparisons. If you compare languages in this way you rapidly enter an overwhelming set (scales an N^2) of idiom-vs-idiom comparisons as you increase the number of languages under your microscope.

So the best approach to linguistic comparison to date is probably the Great Language Shootout. They take the approach that you first get a set of problems that reasonably abstracts the entire set of real-world problems that coders have to deal with. So, we have a few small problems, each representative of some class: binary-trees, k-nucleotide, mandelbrot, etc.. Then we track the performance of each code sample, both in space (memory) and time. Because no single language is suited to all the different problems that can occur, we can find the best-of-breed by adding up the ranks of each language and then sorting. But this only measures computational efficiency, which has long ago gotten so cheap that ordinary mortals don’t waste their time on fancy algorithms [rule 3. under Complexity].

So, what we’d like to track is how efficient the program describes the solution to the problem, and how quickly that solution actually runs. That is we’d like a measure of how naturally a certain language describes the algorithm in addition to how well the language implementation translates that to hardware. So let’s take a lesson from algorithmic information theory, and simplistically take the length of the program (in lines) as a measure of its ability to compress the algorithm into text. (Yes this is really simplistic, a count of tokens going through the lexer would be more appropriate). Then we use a formula (something like):

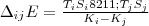
To get a measure of the Time*Space change with program complexity (measured with a length metric), or a measure of the change in efficiency when moving from one language to another. By doing this for the set of problems in the Language Shootout, we can get a feel for what benefits are gained and what abilities lost when translating an algorithm from one language to another. Hopefully this can all be plotted on some sort of manifold, after which we can backtrack to what idioms are most useful for which classes of problems. But this time, with quantitative data to back up the subjective comparisons that we’ve been using to date.

Note: another useful formula for linguistic efficiency might be E=TS/K where we measure the amount of data that can be manipulated per line.

Update: The formulas given really favor languages that have more stuff built-in, or more stuff in their standard lib. I do not thin this is unfair, programmers really enjoy, nay require abstractions in their toolbox. Nobody wants to go implementing yet another linked list every other week, We want that stuff built-in; it increases the language’s expressivity, and standardizes the approach to problems. Weighting in favor of these types of languages is a Good Thing™. Also you’d expect the code that you pull in in this way to be more efficient (general case) than what you’d write yourself. If not, then the formula still penalizes on the Time*Space usage.

Update: I’m wondering wether or not the set of problems chosen by the Language Shootout is a good representative of the class of all problems. Perhaps we should also include some of what might be considered non-language-specific design patterns, like State Machine simulations, Dynamic Programming, Constraint Solving, etc…