Universal Turing Machines, Part 3: Initialization
The first thing we do is scan the machines head all the way over to the Right end of the tape, stopping when we hit a 
, then we’ll have to scan back and copy the designated blank symbol onto the end of the tape, and leave it marked with a
In this manner we shall assure that a symbol is present on the tape when we go to look one up in the encoded transition function.
![\xymatrix @!=3pc {
*++++++++++++[][]{}\ar[dr]{} &*++[][]{ \txt{Copy Blank Symbol Subroutine}}\\
&*++[o][F-]{B_0} \ar[d]_{B \rightarrow B,R}
\ar@(r,u)_{L}\\
&*++[o][F-]{B_1} \ar[dl]_{0 \rightarrow \overline{0},R}
\ar[dr]^{1 \rightarrow \overline{1},R}
\ar[r]^{{\scriptstyle Q \rightarrow Q,L}
\atop
{\scriptstyle \overline{Q} \rightarrow \overline{Q},L}}
\ar@(ul,dl)_{R}
&*++[o][F-]{B_2} \ar[r]^{B \rightarrow B,R}
\ar@(ur,ul)_{{\scriptstyle\overline{0} \rightarrow 0,L} \atop {\scriptstyle\overline{1} \rightarrow 1,L} }& \\
*++[o][F-]{B_3} \ar[dr]_{\Box \rightarrow 0,L}
\ar@(dl,ul)^{R}
&
&*++[o][F-]{B_4} \ar[dl]^{\Box \rightarrow 1,L}
\ar@(dr,ur)_{R}\\
&*++[o][F-]{B_5} \ar[uu]^{{\scriptstyle\overline{0} \rightarrow \overline{0},R} \atop {\scriptstyle\overline{1} \rightarrow \overline{1},R}}
\ar@(dl,dr)_{L}\\
}](http://www.cogitolingua.net/blog/wp-content/plugins/wp-latexrender/pictures/7e1119817739f59d102a5edd08c1718d.png "\xymatrix @!=3pc {
*++++++++++++[][]{}\ar[dr]{} &*++[][]{ \txt{Copy Blank Symbol Subroutine}}\\
&*++[o][F-]{B_0} \ar[d]_{B \rightarrow B,R}
\ar@(r,u)_{L}\\
&*++[o][F-]{B_1} \ar[dl]_{0 \rightarrow \overline{0},R}
\ar[dr]^{1 \rightarrow \overline{1},R}
\ar[r]^{{\scriptstyle Q \rightarrow Q,L}
\atop
{\scriptstyle \overline{Q} \rightarrow \overline{Q},L}}
\ar@(ul,dl)_{R}
&*++[o][F-]{B_2} \ar[r]^{B \rightarrow B,R}
\ar@(ur,ul)_{{\scriptstyle\overline{0} \rightarrow 0,L} \atop {\scriptstyle\overline{1} \rightarrow 1,L} }& \\
*++[o][F-]{B_3} \ar[dr]_{\Box \rightarrow 0,L}
\ar@(dl,ul)^{R}
&
&*++[o][F-]{B_4} \ar[dl]^{\Box \rightarrow 1,L}
\ar@(dr,ur)_{R}\\
&*++[o][F-]{B_5} \ar[uu]^{{\scriptstyle\overline{0} \rightarrow \overline{0},R} \atop {\scriptstyle\overline{1} \rightarrow \overline{1},R}}
\ar@(dl,dr)_{L}\\
}")
Thus our UTM so far looks like
![\xymatrix {
*++[][]{} \ar[r]
&*++[F-]{Start} \ar[r]^{T \rightarrow T,R}
\ar@(ur,ul)_{R}
&*++[o][F-]{Hit \atop Tape} \ar[d]^{\Box \rightarrow \overline{s},L}
\ar@(ur,ul)_{ {\scriptstyle s \rightarrow s,R} \atop {{\scriptstyle 0 \rightarrow 0,R} \atop {\scriptstyle 1 \rightarrow 1,R}} }
\ar[r]^(.4){\overline{s} \rightarrow \overline{s},L}
&*++[F-:<5pt>]{{Lookup\ and} \atop {Copy\ New\ Symbol}}
\\
&
&*++[F-:<5pt>]{{\scriptstyle Copy\ Blank} \atop {\scriptstyle Subroutine}} \ar `l[l] [ul]{}\\
}](http://www.cogitolingua.net/blog/wp-content/plugins/wp-latexrender/pictures/2cdecaaf85cf01975d434c6de93aa3db.png "\xymatrix {
*++[][]{} \ar[r]
&*++[F-]{Start} \ar[r]^{T \rightarrow T,R}
\ar@(ur,ul)_{R}
&*++[o][F-]{Hit \atop Tape} \ar[d]^{\Box \rightarrow \overline{s},L}
\ar@(ur,ul)_{ {\scriptstyle s \rightarrow s,R} \atop {{\scriptstyle 0 \rightarrow 0,R} \atop {\scriptstyle 1 \rightarrow 1,R}} }
\ar[r]^(.4){\overline{s} \rightarrow \overline{s},L}
&*++[F-:<5pt>]{{Lookup\ and} \atop {Copy\ New\ Symbol}}
\\
&
&*++[F-:<5pt>]{{\scriptstyle Copy\ Blank} \atop {\scriptstyle Subroutine}} \ar `l[l] [ul]{}\\
}")
In all of our diagrams the notation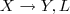 
means the machine will print a Y and move Left if it reads X on the tape. Since we have many symbols in our alphabet 
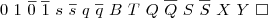the shorthand notation L and R alone on a transition arrow will designate “scan that direction until one of the more interesting transitions occurs”, thus it does not imply nondeterminism. Pedantically it means 
.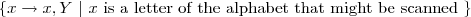