LegoLoom Part 1: Background
The other weekend I experience the pleasure and fascination of visiting the Antique Gas and Steam Engine Museum. While there, my friend and I perused the loom room Weaver’s Barn. At first, I’m shocked that people spend time weaving, as it looks like such a task should be fully mechanized. We’ll get to that in the history section!

Being of a technical inclination, I went around the shop floor looking at the different loom setups. They all share some common features: foot bars connected to shafts that move groups of threads up and down to make the pattern of the weave, a shuttle to pass thread across, a big comb to press the horizontal threads into the cloth, a roller of threads on the back and another roller of threads on the front. Plenty of the loom used thick threads, like yarn, and some even had ribbon for the horizontal thread, weaving what looked like a rug or mat.
All but one of the looms controlled the weave pattern via a sequence of shafts that group the heddles. Those designs produce a recurrent pattern, typically a repeating one like plain weave, twill, or houndstooth. But I see a weave — an over or under — as a pixel, and a machine with 4, 6, or even 12 shafts simply can’t produce arbitrary patterns like this woven portrait of Jacquard — woven from a program of 24,000 punched cards in 1839.

By Michel Marie Carquillat (tisseur) d’après Claude Bonnefond – Link
I simply can’t resist injecting here that the most awesome part about that picture is the meta-referential inclusion of the loom in the background and cards in the foreground!
What makes Jacquard and his loom so special?
From a wonderful TV series, Connections, presented by James Burke, that I recall watching an episode about the Jacquard loom. Mention of the machine also occasionally occurs in the history of Computer Science, because we attribute credit for it being the first programmable machine, weaving from a program of punch cards.
If you can program the weave as you would a grid of pixels, then you can make a pattern that doesn’t repeat! Very early on, this ability got used for Jacquard’s portrait and other imagery as part of bespoke fabric design. Although I remain quite impressed by the ability of the loom, specifically its importance as a stepping stone in the history of computing, I can’t help but notice that the programmed sequence is just… longer. It still loops!
In the case of Jacquard’s portrait, keep using the card stack and we’d cycle through and producing an endless sequence of the same portrait. A very large for-loop over a fixed pattern. In 1800’s England they didn’t have a formalized notion of a non-repeating pattern.
A new shape dropped this year!
Earlier this year, a few mathematical tinkerers discovered the Einstein Tile! Actually, they found a whole parameterized family of aperiodic monotiles! Shortly afterward, they followed up with the Spectre, fixing an itch to avoid reflections.
Shoot. I got excited. Let’s back up to 1961, when Wang worked on the Domino Problem — Whether a set of square tiles with a color on each side can cover the plane without rotation or reflection when placed side by side with matching colors.
By Claudio Rocchini – Own work, CC BY-SA 3.0, Link
In 1966, Berger solved the problem by showing how translate any Turning Machine into a set of Wang tiles that tiles the plane if and only if the Turning Machine does not halt, thus demonstrating that no algorithm can decide an answer for all tile sets. So much more info is at Wikipedia.
The original work needed 20426 tiles and obviously weren’t drawn but only described. In 1971, Robinson worked the number down to 52 tiles. Work in 2015 reduced it further to a set of 11.

But the original solution led to a yet more interesting observation: There must exist a finite set of Wang tiles that covers the plane, but only does so without periodicity. This launched inquiry into finding such tile sets, and more generally tile shapes that tile the plane, but without periodicity.
In the List of aperiodic sets of tiles you can see how most of the approaches have tiles with rules — dots, colors, etc — that restrict the matching of edges. By 1971, Penrose famously discovered 2 shapes that would tile the plane aperiodically. And there we stood for 50 years.

By Solarflare100 – Own work, CC BY 3.0, Link
Again! The meta-referentiality here is delicious. That’s Roger Penrose in the foyer of the Mitchell Institute for Fundamental Physics and Astronomy, Texas A&M University, standing on a floor with a Penrose tiling.
Earlier this year, we got a new shape! An Einstein Tile! One Stone that tiles the plane aperiodically! They called it The Hat. It’s beautiful in simplicity and the proof is by fractal construction.
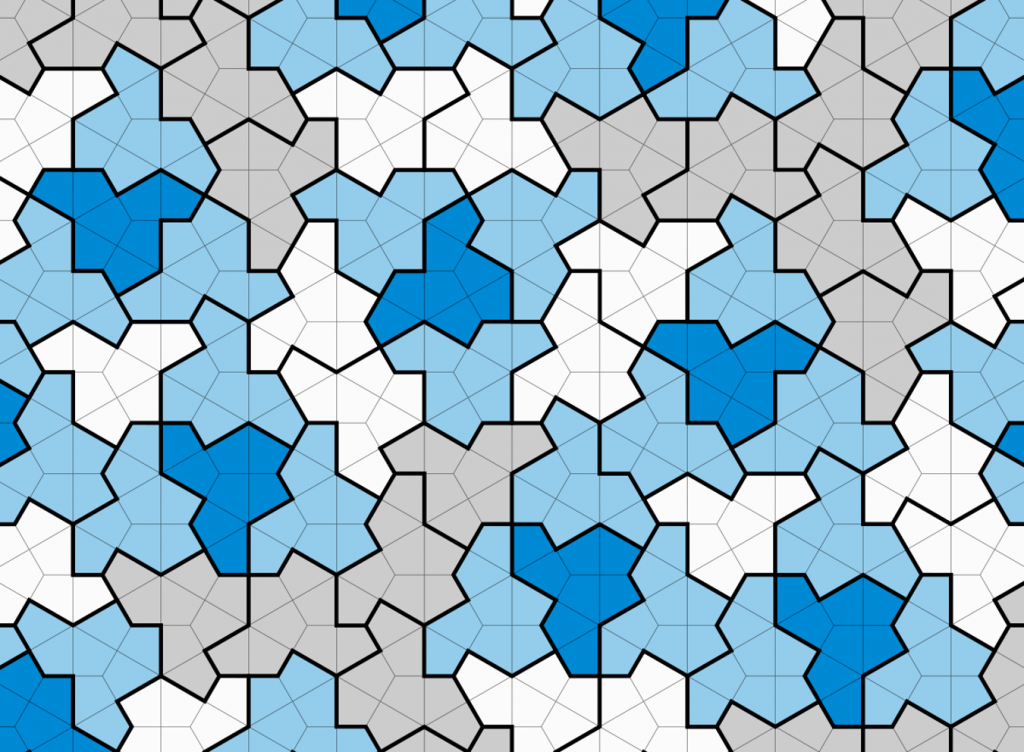
I was really excited by this work! Seriously I told everyone I met for about 2 weeks after I heard about it. And I went and read the proof! I mean, how often is it that we get a large breakthrough that occurs on a kitchen table? Or with a shape that comes from combining 4 darts found in a common toy tile set for children?
But, I had an issue with this tiling, because it sometimes uses a reflection. While technically not against the rules, it’s an itch. The discover’s agreed, because within a couple months they found a chiral aperiodic monotile called The Spectre! With straight edges, it also admits a periodic tiling, but curving or notching the edges forces only aperiodic tilings.

A return to the loom
Given that the aperiodic tiling is so simple, yet deviously complex in its coverage of the plane, it makes for a beautiful challenge of a Jacquard loom! But this time, we can’t have a loop of punchcards. Instead, we must compute each scanline of the tiling.
So I went back and looked at the Jacquard loom in the Weaver’s barn. It could be done by creating a box that presents a set of holes, dynamically acting as a new card for each line of fabric.
We can definitely create such a box with solenoids and an arduino. Even though I’m not strong in the computer graphics department, I’m pretty sure I could learn how to program a tiling and then raster scan it for producing lines of fabric. But that approach uses modern tech attached to an old device.
If they had known about such a thing, could someone in 1800 have produced an aperiodic pattern by purely mechanical means? I think so, but we’d have to pick an even simpler pattern.
Cellular Automata, Rule 30
Back in the early 2000s, Wolfram published A New Kind of Science, a book about trying to find the laws of physics in very simple rule structures like cellular automata. I read that book (but not all the footnotes, which were even larger in word count than the main text).
| Current pattern | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
| New state for center cell | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
A very simple rule. Computable with a few gears! They had those in 1800. I did a K-map that works out to (!L and R) or (!L and C) or (L and !C and !R) for left, center, and right. Not very many logic operations at all. Completely achievable with 1800s technology!
Turns out this rule is Turing Complete and produces an aperiodic pattern.

The Jacquard Project
Use 1800s tech to compute an aperiodic pattern, and weave it on an old Jacquard just as they would have done.
OK, so it won’t be the prettiest of fabrics. And the arbitrarily long runs of the same pixel setting means instability in the weave. But the more troublesome part: I’ve got a problem with the fabric being of fixed width on the loom, so I’ll have to choose — anchor to 0, anchor to 1, or do a computation. I’ll write up a program to exercise the visuals, but I’m tempted to use a mod 2 checksum or some other simple trick that’ll introduce a random element into the fabric. Maybe hold a register with one lookback and just “bounce off the wall”.
OK, so caveat. Even with a modern loom, you do eventually run out of warp threads. Although I could image a world with 10k spinners behind a machine so that doesn’t happen for as long as you can feed it raw wool. But hypothetically solving that, you’d still cut off the fabric for sale. So you might as well just run a loop on a pre-computed image that’s only as long as the warp lasts, or even shorter, as long as the reams being sold.
So technically, in 1800 they would have pre-computed a reasonable size of Rule 30 and run a sequence of cards. But I’m gonna use Lego gears and logic gates.
This is something they could have done in 1800 but for:
- They didn’t have knowledge of Rule 30, by circumstance of not having developed that branch of mathematics (contingent on computers for quick experimentation).
- They hadn’t yet developed the perspective of seeing problems from a computational perspective — Modulo Charles Babbage, who was very clearly inspired by Jacquard looms and owned one of those woven portraits.
Modern Looms
Alright. I dove into loom technology for a couple of days after the museum visit. Modern mechanized looms are awesome. Fully programmable, fully automated, extremely fast. Did you know they got rid of the shuttle!?! Now they just blast the string through the air!
I still really want this bedspread.


Note: Here’s a really descriptive page about [Tesselations](https://creatureandcreator.ca/?p=5803), including graphical instructions for creating the einstein tile!